小明在假期召唤了一只恶魔。因为闲得无聊，他就和恶魔聊天。恶魔：“你抛一枚硬币，正面你将获得1元，背面你将失去1元，交易吧~。”小明想了想：“爽快点！我有99.999%的概率赢1万，没赢就赔给你10亿！”恶魔也蛮好说话，同意了。于是......

        好，现在有没有人想召唤这只恶魔呢？俗话说，money is the root of all evil。只要你有钱，就可以在任意一家赌场召唤牠——使用马丁格尔策略。

        什么是马丁格尔策略？其实一定有不少朋友早就想到过——很简单，就是输钱后翻倍加注直到把钱赢回来为止。比方说我先投1元，如果赔了就再投2元，继续赔就继续投4元。如此操作，自然早晚有压中的一天，那时你就把最初的本金赚回来了——1元

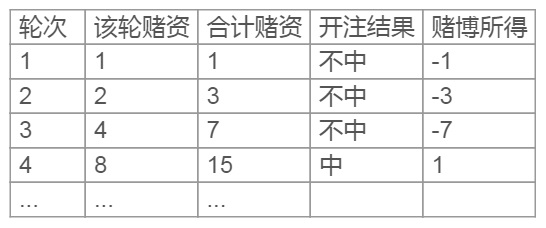
        我们来分析分析这个策略。额......由于这个方法太过简单粗暴，其实也没有什么好分析的。明眼人都能看出这种特殊的押注策略可以在期望仍然为零的情况下，通过减小每次赢钱所得，而把亏损概率压缩至一个非常小的程度。比如我以10轮为一组执行马丁格尔策略，以1元为初始赌资，翻倍押注，一次胜利后就收手；如果连续10次不中，就强制结束。这样我就需要1023元总赌资，有1023/1024的概率赢得1元，1/1024的概率亏损1023元。

        简而言之，我们这样一“包装”，赢钱的概率上去了，但输钱的成本也增加了。不过没关系，有些人就是喜欢刺激~如果借助马丁格尔策略的基本思想，加以其它各种金融、数学工具的辅助，我们甚至可以把输钱概率下降到不大于车祸概率的程度。世事无常，如果有人连这点概率都承担不起的话，他就不用过马路了。

        当然，我们也发现这种策略的弊端在于需要大量资金支持。如何利用较少的钱把失败概率“压缩”到更低的程度就是挺有意思的一个研究话题。在不考虑杠杆的情况下，由于期望为0，我们的总赌资就是所亏金额的最大数目。所以如果你有x元本金，每一组操作想赚y元，那么你赔光本金的概率就是 y/(x+y) 。什么？你说你不知道如何自由控制y的值？还是以10轮一组，1023元本金为例——只要你有2047元本金，就可以同时进行10组这样的操作。言至于此，具体如何操作自己琢磨吧~

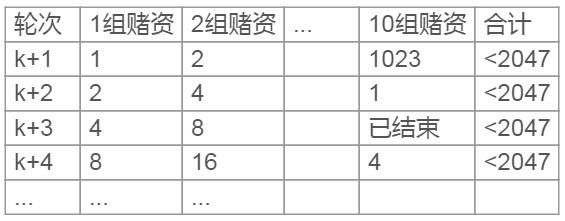
        说完马丁格尔策略，我们顺便来看看反马丁格尔策略：赢钱就翻倍加注，输钱就减为1注，达到预定目标就收手——刚好和马丁格尔策略反着来。这种策略期望同样为0，会出现连续不断赔钱的状况；可一旦运气来了，1变2，2变4，4变8......理论上如果赌资充足，也的确有很大概率达到目标。在此不做太多讨论。